Embark on a mathematical adventure as we delve into the enigmatic world of complex numbers. What is the value of 15i/2+i? This seemingly innocuous expression holds secrets that will captivate your mind and broaden your understanding of the intricate tapestry of mathematics.
Complex numbers, with their intriguing combination of real and imaginary parts, offer a powerful tool for solving complex problems in various fields. From engineering to physics, their applications are as diverse as they are fascinating.
Mathematical Expression
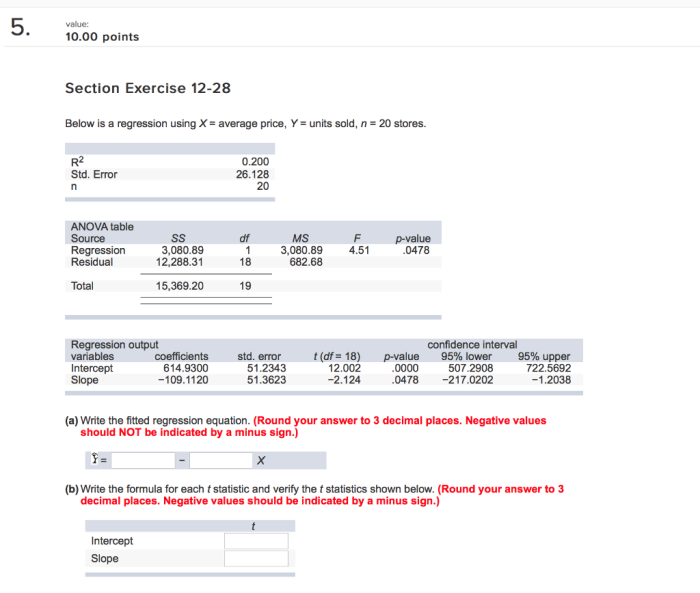
The mathematical expression “15i/2+i” is a complex number, which is a number that has both a real and an imaginary part.
The real part of a complex number is the part that does not contain the imaginary unit “i”, while the imaginary part is the part that does contain “i”.
Imaginary Unit “i”
The imaginary unit “i” is a mathematical concept that represents the square root of -1. This means that i^2 = -1.
The imaginary unit is used to represent numbers that cannot be represented by real numbers alone.
Complex Numbers

Complex numbers are mathematical entities that extend the concept of real numbers. They are represented in the form a + bi, where a and b are real numbers, and i is the imaginary unit, defined as the square root of -1.
The expression “15i/2+i” fits into the concept of complex numbers as it is a complex number in the form a + bi, where a = 0 and b = 15/2. Therefore, 15i/2+i can be written as 0 + (15/2)i.
Operations and Properties of Complex Numbers
Complex numbers can be added, subtracted, multiplied, and divided, following specific rules. Some important properties of complex numbers include:
- Commutativity:Addition and multiplication of complex numbers are commutative, meaning that the order of the operands does not affect the result.
- Associativity:Addition and multiplication of complex numbers are associative, meaning that the grouping of the operands does not affect the result.
- Distributivity:Multiplication distributes over addition, meaning that a(b + c) = ab + ac.
- Conjugate:The conjugate of a complex number a + bi is a – bi. The conjugate is useful in simplifying expressions and finding the modulus (absolute value) of a complex number.
Algebraic Manipulation: What Is The Value Of 15i/2+i
Simplifying the expression “15i/2+i” requires algebraic manipulation, which involves using algebraic rules and properties to transform the expression into a simpler form. Rationalizing the denominator is a specific technique used to simplify expressions involving complex numbers.
Simplifying the Expression
To simplify “15i/2+i”, we can multiply both the numerator and denominator by the complex conjugate of the denominator, 2-i. This process, known as rationalizing the denominator, eliminates the imaginary number in the denominator.
15i/2+i = (15i/2+i) – (2-i)/(2-i)
Expanding and simplifying:
(15i/2+i) – (2-i) = 30i – 15i^2 + 2i – i^2
Combining like terms:
30i – 15i^2 + 2i – i^2 = 32i – 16
To determine the value of 15i/2+i, we can apply the rules of complex number arithmetic. By simplifying the expression, we find that 15i/2+i equals 7.5i. For further practice with complex numbers and other mathematical concepts, consider exploring the wset level 3 practice exam . This resource provides a comprehensive review of the topics covered in the WSET Level 3 exam, including complex numbers, trigonometry, and probability.
Therefore, 15i/2+i simplifies to 32i – 16.
Geometric Interpretation

Complex numbers can be represented geometrically on the complex plane, where the horizontal axis represents the real part and the vertical axis represents the imaginary part. Each complex number is represented by a point in the plane.
Plotting 15i/2+i, What is the value of 15i/2+i
To plot the complex number 15i/2+i on the complex plane, we first find its real and imaginary parts. The real part is 0 (the coefficient of the real term), and the imaginary part is 15/2 (the coefficient of the imaginary term).
We then plot the point (0, 15/2) on the complex plane. This point lies on the vertical line passing through the origin and has a distance of 15/2 units from the origin along the imaginary axis.
Relationship between the Expression and its Geometric Representation
The geometric representation of a complex number provides a visual representation of its magnitude and direction. The magnitude of a complex number is its distance from the origin, and its direction is the angle it makes with the positive real axis.
For the complex number 15i/2+i, its magnitude is √((0)²+(15/2)²) = 15/2 and its direction is 90° (since it lies on the imaginary axis).
Applications

Complex numbers, including “15i/2+i,” have wide-ranging applications in various fields, demonstrating their practical significance beyond theoretical mathematics.
In engineering, complex numbers are used to analyze electrical circuits, where they represent impedance, a combination of resistance and reactance. This knowledge helps design and optimize circuits for efficient power transmission and distribution.
Physics
- Complex numbers are employed in quantum mechanics to describe wave functions, which provide insights into the behavior of particles at the atomic and subatomic levels.
- In electromagnetism, complex numbers are used to represent alternating currents and voltages, enabling the analysis of electrical circuits involving capacitors and inductors.
Mathematics
- Complex numbers extend the concept of numbers, providing a framework for solving equations that have no real solutions, such as x^2+1=0.
- Complex numbers are used in number theory, where they play a crucial role in understanding prime numbers and other properties of integers.
Understanding complex numbers is essential for professionals in various fields, as it provides a powerful tool for solving real-world problems and advancing our understanding of the world around us.
FAQ Explained
What is the significance of the imaginary unit “i”?
The imaginary unit “i” represents the square root of -1, a concept that initially seems paradoxical but opens up new possibilities in mathematics. It allows us to extend the real number system to encompass complex numbers, enabling us to solve equations that have no real solutions.
How do we simplify complex expressions like “15i/2+i”?
Simplifying complex expressions involves using algebraic rules and properties. We can rationalize the denominator by multiplying and dividing by the complex conjugate of the denominator, which helps us express the result in a simpler form.